Vector algebra correspond to the extension of a linear space, Rn, dimension n, to a linear space Cln, dimension 2^n (2 power n), composed with multivectors.
Multivectors are obtained by linear combination of exterior products of basis elements from vector space Rn.
A multivector is an extension at superior dimensions of the notion we have about vectors.
Evalgebra support Cl1 to Cl5 with arbitrary signature.
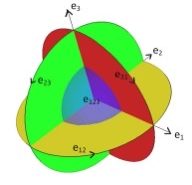
As exemple, Cl3 has a basis obtained by external products of canonical basis vectors (e1, e2, e3) from R3, and a unit scalar e0 (=1).
e1 . e1 = e2 . e2 = e3 . e3 = 1 and e1 . e2 = e1 . e3 = e2 . e3 = 0 (scalar products)
e1 ^ e2 = – e2 ^ e1, e2 ^ e3 = – e3 ^ e2, e1 ^ e3 = – e3 ^ e1, e1 ^ e2 ^ e3 = – e3 ^ e2 ^ e1 (exterior products)
e1 ^ e2 may be represented as an oriented square area with sides e1, e2 or by a disk, or any other shape with same area and orientation. e2 ^ e1 is the same square (or disk …) with reverse orientation.
e1 ^ e2 ^ e3 oriented volume (cube, or sphere …).
Cl3 basis vectors :
a scalar (0-vector) e0
vectors (1-vector) e1, e2, e3
bivectors (2-vector) e12, e23, e13
trivector (3-vector) e123
e12 is short script for e1 ^ e2 etc … (eij with i<j), e123 for e1 ^ e2 ^ e3.
An element of Cl3 is a linear combination of these basis elements :
A = a0*e0 + a1*e1 + a2*e2 + a3*e3 + a12*e12 + a23*e23 + a13*e13 + a123*e123 with ai real numbers.
number of basis elements in Cln :
n|_____ grade k ___
0| 1
1| 1 1
2| 1 2 1
3| 1 3 3 1
4| 1 4 6 4 1
5| 1 5 10 10 5 1
…| …
setting the basis in Evalgebra :
command Cl(p,q) with p+q basis vectors, p positive squares, q negative squares.
ex : Cl(2) -> p=2, q=0 oriented volume = e12 e1²=e2²=1 signature = (1,1)
Cl(3,1) -> p=3, q=1 oriented volume = e1234 e1²=e2²=e3²=1 e4²=-1 signature = (1,1,1,-1)
Cl(2,2) -> p=2, q=2 oriented volume = e1234 e1²=e2²=1 e3²=e4²=-1 signature = (1,1,-1,-1)
Some usefull operators :
grade operator :
grade(A,k) =k gives the k-vector )part of A
as example, if A = 3e0 + 2e1 – e2 + 2e23,
grade(A,0) = 3e0
grade(A,2) = 2e23
grade(A,1) = 2e1 – e2
grade(A,0)+grade(A,1) = 3e0 +2e1 -e2
reversion :
reversing basis element order :
e0 -> e0, e1 -> e1, …, e12 -> e21 (= -e12), e23 -> e32 (= -e23) etc …
ex : rev(A) = 3e0 +2e1 –e2 -2e23
grade involution :
changing basis element direction :
e1 -> -e1, e2 -> -e2 …, e12 -> -e1 ^ -e2 (=e12) etc …
ex : invol(A) = 3e0 -2e1 +e2 +2e23
Clifford conjugation :
cj(A) = invol(rev(A)) = rev(invol(A))
ex : cj(A) = 3e0 -2e1 + e2 – 2e23
The products :
exterior product « ^ » caracterize vector sub-spaces generated by a family of free k-vectors.
As example, mutiplying two independant vectors a1*e1 ^ a2*e2, we get a bivector a1* a2*e12, and multiplying this bivector by an independant vector a3*e3 we get a trivector a1*a2*a3*e123.
inner product « . » correspond to the generalisation to the multivector set of orthogonality notion, as we know with the scalar product of vectors.
So, if two k-vectors are orthogonal, their inner product is 0.
geometric product » « for two vectors is the sum of their inner product and exterior product
u v = u.v + u^v
If two vectors are orthogonal, the scalar product is 0 and the geometric product is equal to the external product : u v = u^v
If u and v are colinear, the externior product is 0 and the geometric product equal to the scalar product. u v = u.v
Generaly, vectors are betwen these two cases, and the geometric product encode the notion of relative direction and magnitude betwen the vectors.
The geometric product may be interpreted also as an operator : w = u v v transform –> w
inner and outer products may be expressed as functions of geometric product :
u.v = 1/2(u v + v u)
u^v = 1/2(u v – v u)
u ⊥ v ==> u v = – v u (u and v anticommute = orthogonal)
u // v ==> u v = v u (u and v commute = colinear)