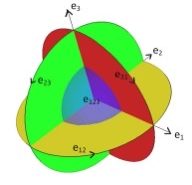
define basis e0,e1,e2,e3,e12,e13,e23,e123
define 2 vectors a=(3,2,-1) and b=(3,0,-5)
geometric product a b
inner product a.b
outer product a^b
define multivector Cl(3) B=(3,1,-5,0,1,2,0,0)
grade projection : scalar <B,0>
vector <B,1>
bivector <B,2>
pseudoscalar <B,3>
involutions : reversal
grade involution
Clifford conjugation
inverse 1/B
dual B*
magnitude |B|
normalize B/|B|
Cl(3)
a=3e1+2e2-e3 and b=3e1-5e3
gp(a,b)
inp(a,b)
outp(a,b)
B=3e0+e1-5e2+e12+2e13
grade(B,0)=3e0
grade(B,1)=e1-5e2
grade(B,2)=e12+2e13
grade(B,3)=0
rev(B)=3e0+e1-5e2-e12-2e13
invol(B)=3e0-e1+5e2+e12+2e13
cj(B)=3e0-e1+5e2+e12+2e13
inverse(B)
dual(B)
magnitude(B)
normalize(B)
More functions
Sin1() cos1() tan1()
sinh1() cosh1() tanh1()
pow1() exp1() log1()
asin1() acos1() atan1()
asinh1() acosh1() atanh1()
Inner products :
Left contraction
Rigth contraction
Hestenes inner product
inp()
rc()
doth()
utilitaires :
dsp(a)
disp(a)
print(« text », expression)
rnd(a)
rnd1(a), rnd2(a), rnd3(a), rnd4(a), rhd5(a), rnd6(a)
info
check(expression1==expression2)
_
display a in vector format like (3,0,2,0,0,7,-7,0)
display a by grade
display results
round to 3 decimals
round to n decimals
Information on context
stop program if false (==, >, <, …)